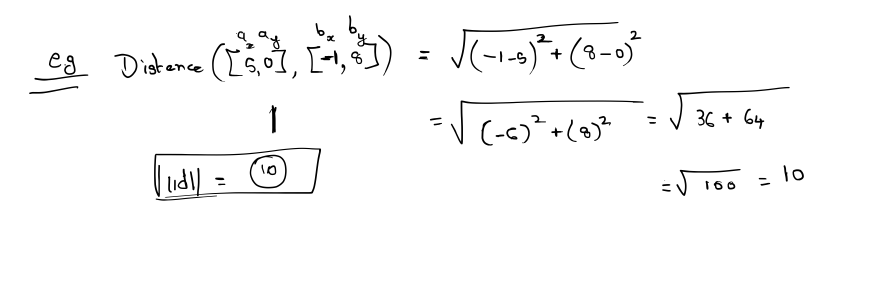
Vector
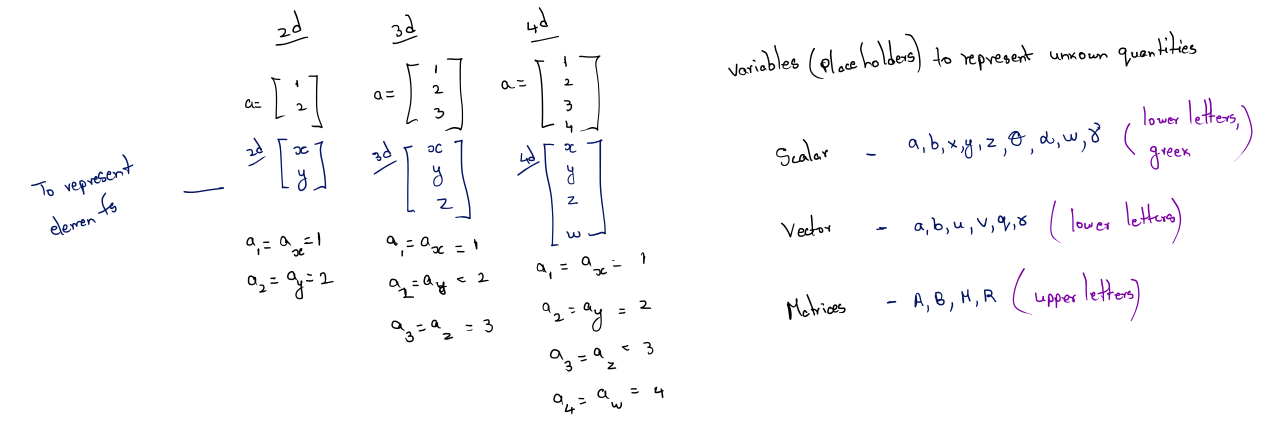
To mathematicians, a vector is a list of numbers. Programmers will rec- ognize the synonymous term array. Notice that the STL template array class in C++ is named vector, and the basic Java array container class is java.util.Vector. So mathematically, a vector is nothing more than an array of numbers.
Let’s begin with understanding some basic principles of number systems and the first law of computer graphics.
The dimension of a vector tells how many numbers the vector contains. Vectors may be of any positive dimension, including one. In fact, a scalar can be considered a 1D vector. In this , we primarily are interested in 2D, 3D, and (later) 4D vectors.
When writing a vector, mathematicians list the numbers surrounded by square brackets, for example, [1,2,3].
When we wish to refer to the individual components in a vector, we use subscript notation. In math literature, integer indices are used to access the elements.
Geometric Definition of Vector
A vector is a directed line segment that has magnitude and direction.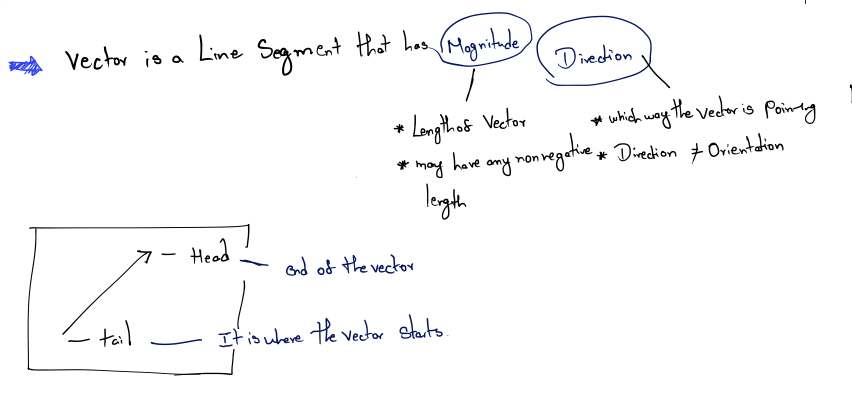
Where is this vector? Actually, that is not an appropriate question. Vectors do not have position, only magnitude and direction. This may sound impossible, but many quantities we deal with on a daily basis have magnitude and direction, but no position. Consider how the two statements below could make sense, regardless of the location where they are applied.
Notice that displacement and velocity are technically different from the terms distance and speed. Displacement and velocity are vector quantities and therefore entail a direction, whereas distance and speed are scalar quan- tities that do not specify a direction.
More specifically, the scalar quantity distance is the magnitude of the vector quantity displacement, and the scalar quantity speed is the magnitude of the vector quantity velocity.
Difference between Scalar Quantity and Vector Quantity
Specifying Vectors with Cartesian Coordinates
When we use Cartesian coordinates to describe vectors, each coordinate measures a signed displacement in the corresponding dimension. For ex- ample, in 2D, we list the displacement parallel to the x-axis, and the dis- placement parallel to the y-axis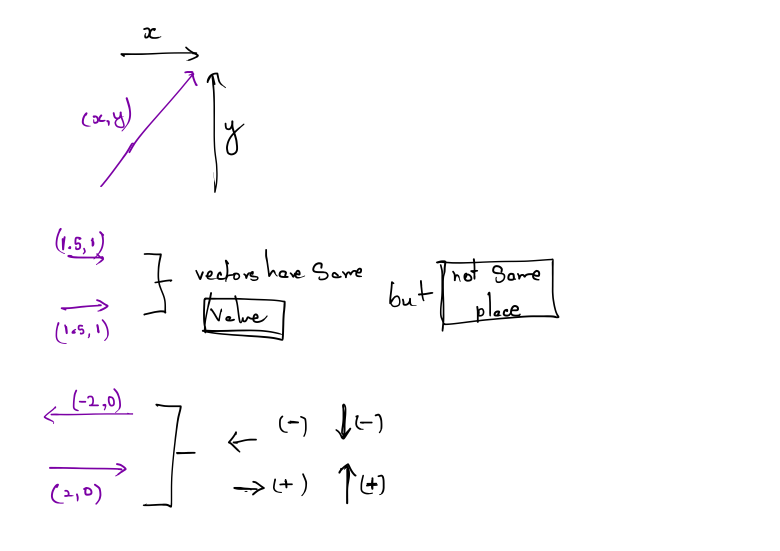
Vector as a Sequence of Displacements
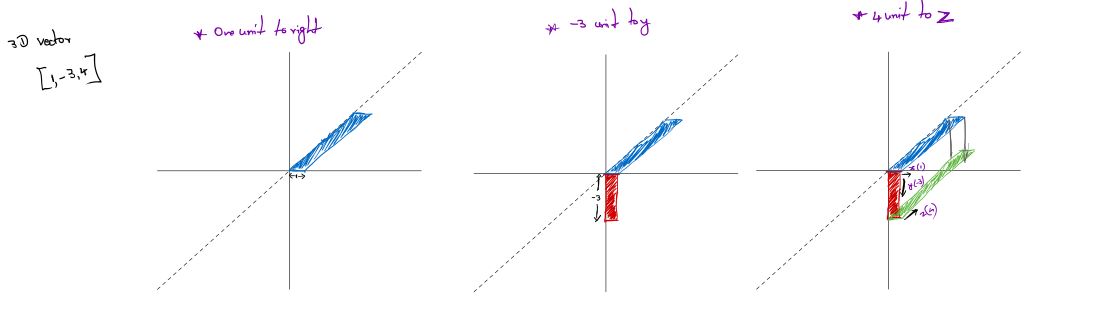
The 3D vector [1,−3,4] represents a single displacement, but we can visualize this displacement as moving 1 unit to the right, 3 units down, and then 4 units forward.
Vectors versus Points
Recall that a “point” has a location but no real size or thickness. In this chapter, we have learned how a “vector” has magnitude and direction, but no position. So “points” and “vectors” have different purposes, conceptually:“point” specifies a position, and a “vector” specifies a displacement.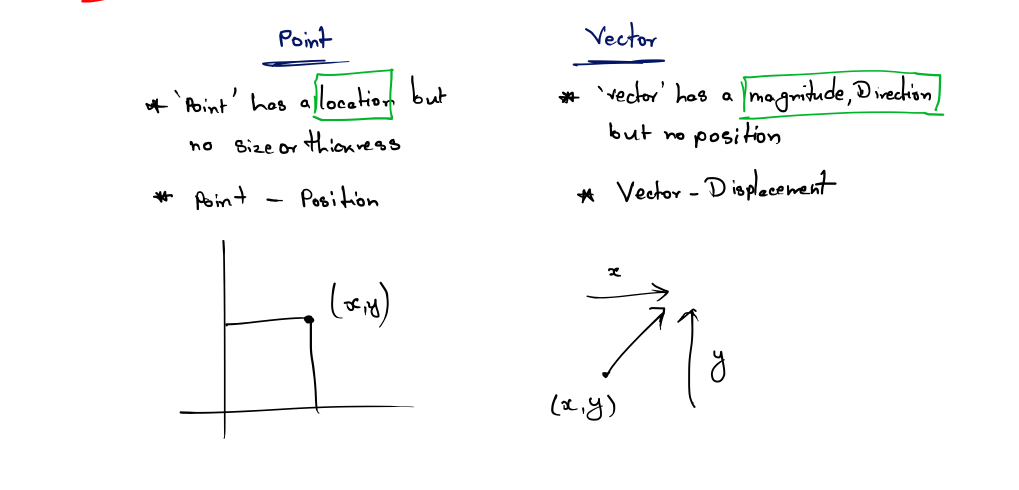
Negating a Vector
Let’s dust it off. For any group, the additive inverse of x, denoted by −x, is the element that yields the additive identity (zero) when added to x. Put simply, x + (−x) = 0. Another way of saying this is that elements in the group can be negated.The negation operation can be applied to vectors. Every vector v has an additive inverse −v of the same dimension as v such that v + (−v) = 0.
Linear Algebra Rules
To negate a vector of any dimension, we simply negate each component of the vector.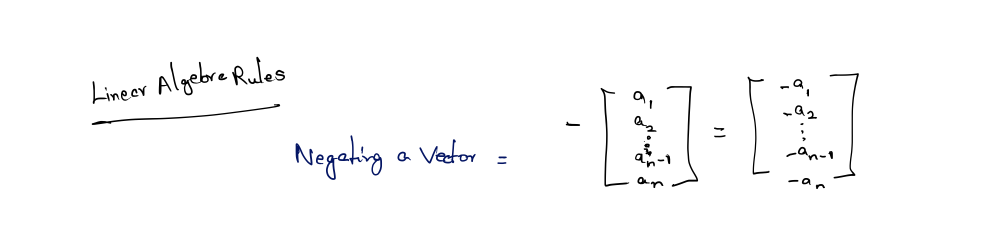
Applying this to the specific cases of 2D, 3D, and 4D vectors
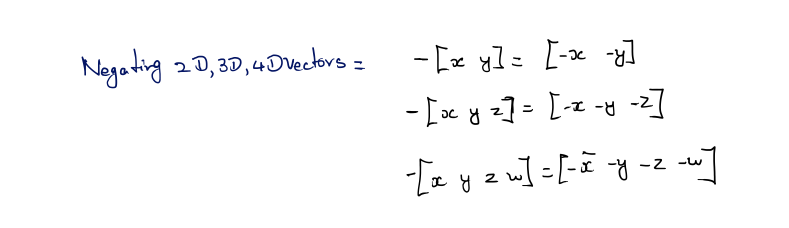
Vector Multiplication by a Scalar
we cannot add a vector and a scalar, we can multiply a vector by a scalar. The result is a vector that is parallel to the original vector, with a different length and possibly opposite direction.
Linear Algebra Rules
Vector-times-scalar multiplication is straightforward; we simply multiply each component of the vector by the scalar. Stated formally,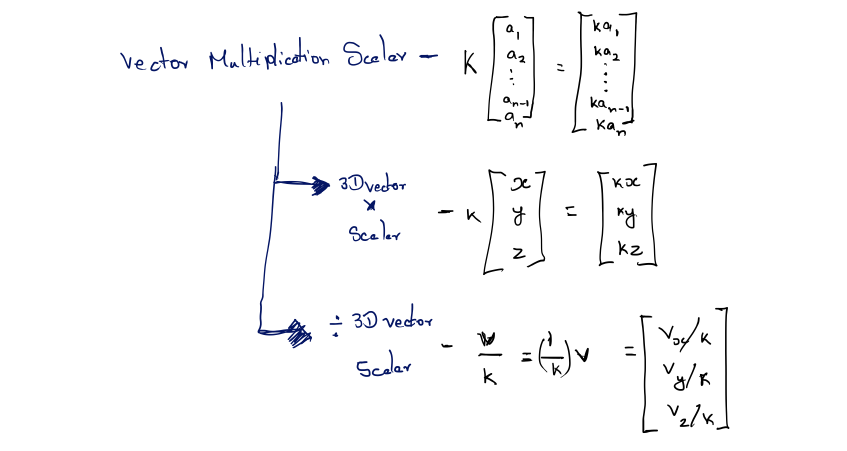
Vector Addition and Subtraction
We can add and subtract two vectors, provided they are of the same dimen- sion. The result is a vector quantity of the same dimension as the vector operands. We use the same notation for vector addition and subtraction as is used for addition and subtraction of scalars.
Linear Algebra Rules
The linear algebra rules for vector addition are simple: to add two vectors, we add the corresponding components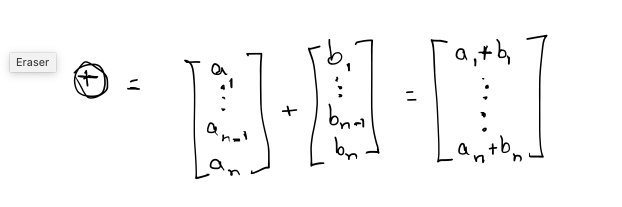
Subtraction can be interpreted as adding the negative, so a − b = a + (−b):
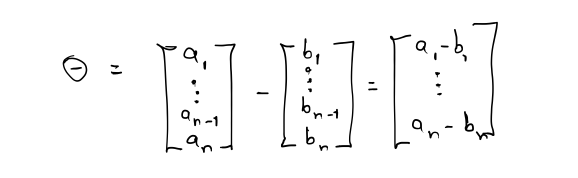
addition and subtraction of scalars, vector addition is commutative,
Geometric Interpretation
We can add vectors a and b geometrically by positioning the vectors so that the head of a touches the tail of b and then drawing a vector fromthe tail of a to the head of b. In other words, if we start at a point and apply the displacements specified by a and then b, it’s the same as if we had applied the single displacement a + b. This is known as the triangle rule of vector addition.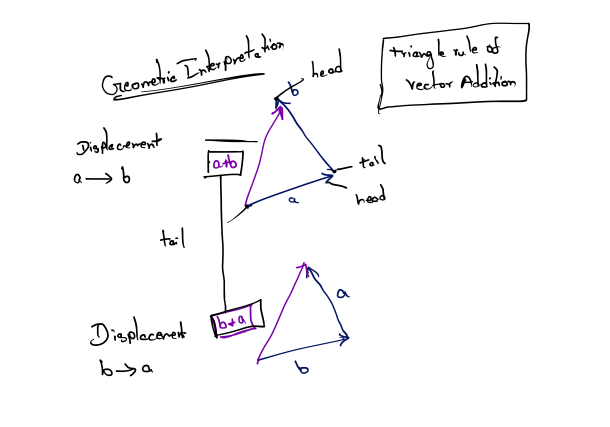
Vector Magnitude
Vectors have magnitude and direction. However, you might have noticed that neither the magnitude nor the direction is expressed explicitly in the vector.
For example, the magnitude of the 2D vector [3, 4] is neither 3 nor 4; it’s 5. Since the magnitude of the vector is not expressed explicitly, we must compute it. The magnitude of a vector is also known as the length or norm of the vector.
Linear Algebra Rules
In linear algebra, the magnitude of a vector is denoted by using double vertical bars surrounding the vector.This notation and the equation for computing the magnitude of a vector of arbitrary dimension n
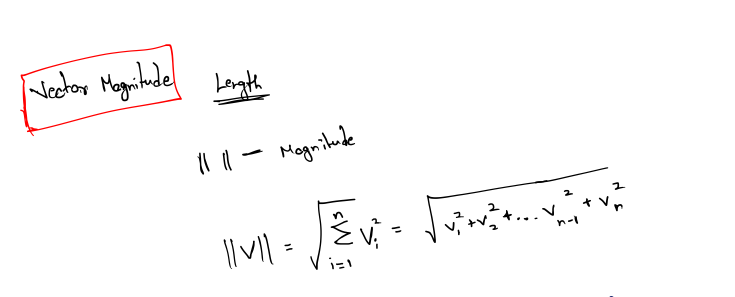
Thus, the magnitude of a vector is the square root of the sum of the squares of the components of the vector
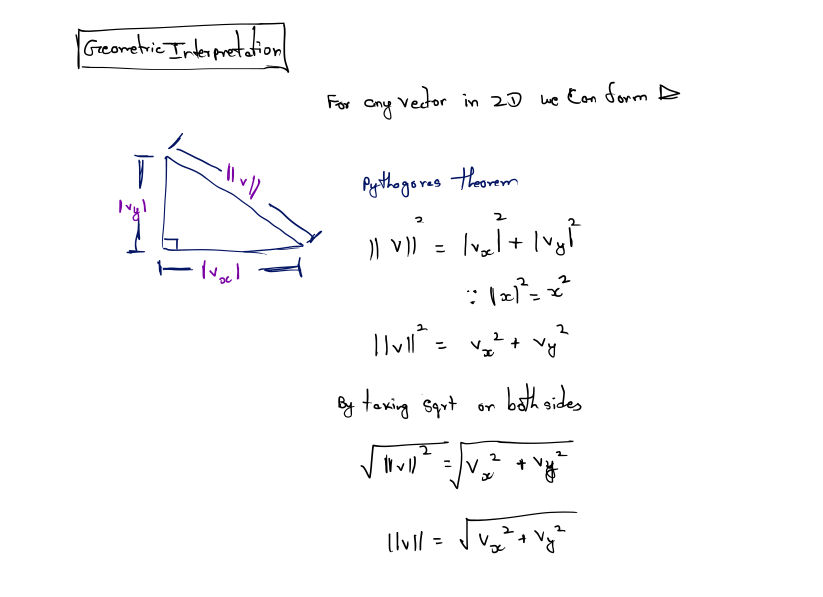
Geometric Interpretation
we had to put absolute value signs around the components vx and vy . The compo- nents of the vector may be negative, since they are signed displacements, but length is always positive.The Pythagorean theorem states that for any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Applying this theorem.
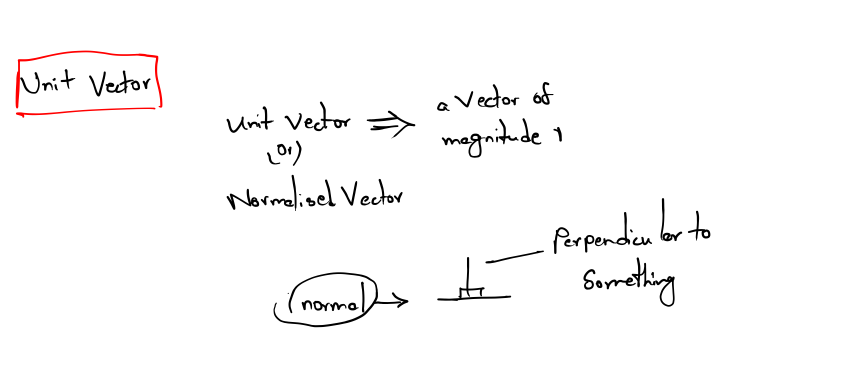
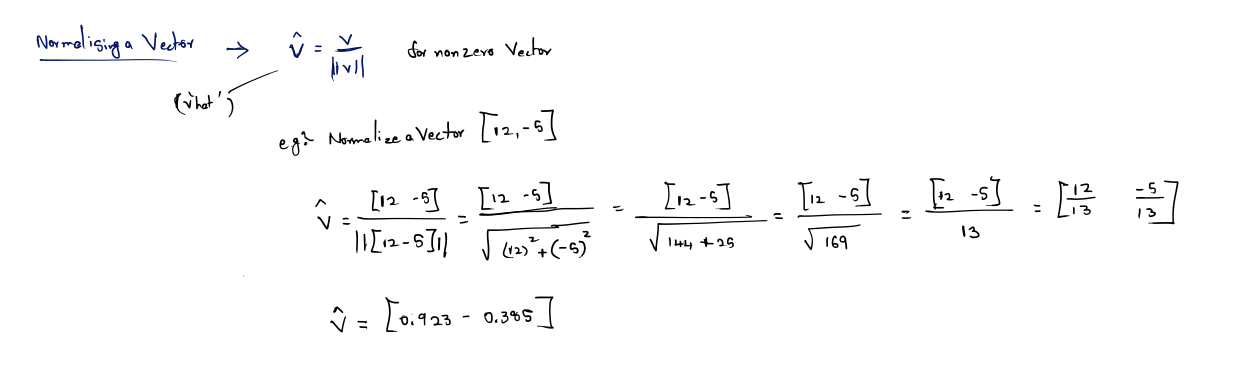
Unit Vectors
For many vector quantities, we are concerned only with direction and not magnitude: “Which way am I facing?” “Which way is the surface ori- ented?” In these cases, it is often convenient to use unit vectors.
A unit vector is a vector that has a magnitude of one. Unit vectors are also known as normalized vectors.
For any nonzero vector v, we can compute a unit vector that points in the same direction as v. This process is known as normalizing the vector. In this book we use a common notation of putting a hat symbol over unit vectors; for example, vˆ (pronounced “v hat”). To normalize a vector, we divide the vector by its magnitude:
Distance Formula
We are now prepared to derive one of the oldest and most fundamental formulas in computational geometry: the distance formula. This formula is used to compute the distance between two points.
First, let’s define distance as the length of the line segment between the two points. Since a vector is a directed line segment, geometrically it makes sense that the distance between the two points would be equal to the length of a vector from one point to the other.
Let’s derive the distance formula in 3D. First, we will compute the vector d from a to b
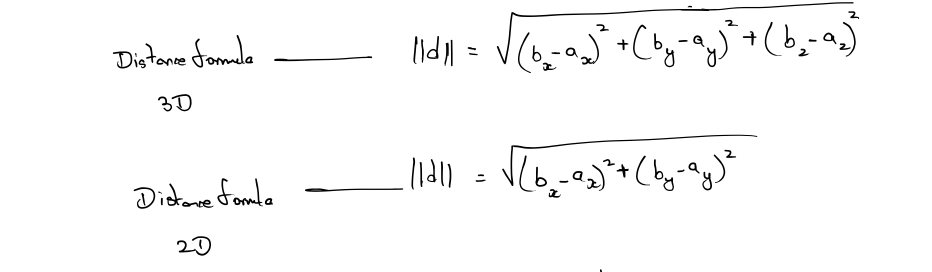
For Example
