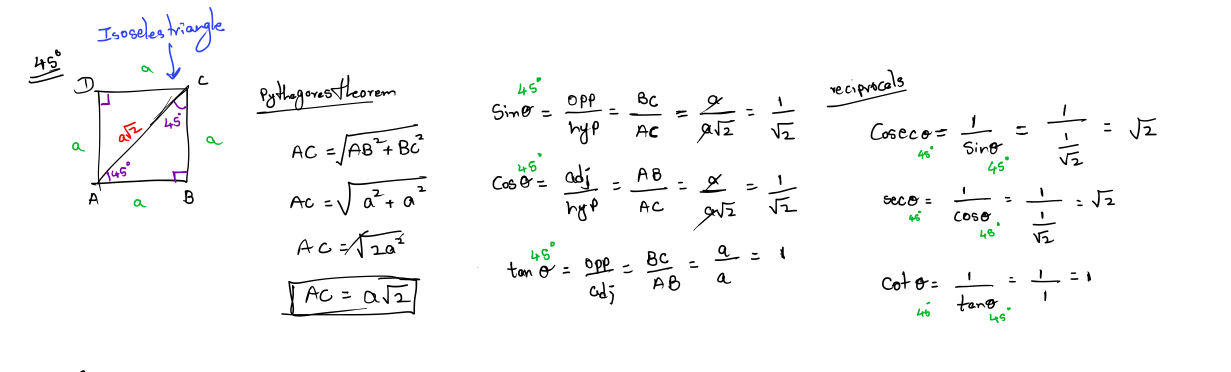
Cartesian Coordinate Systems
3D math is all about measuring locations, distances, and angles precisely and mathematically in 3D space. The most frequently used framework to perform such calculations using a computer is called the Cartesian coordinate system.
Let’s begin with understanding some basic principles of number systems and the first law of computer graphics.
If it looks right, it is right.
The First Law of Computer Graphics
1D Maths
The natural numbers, often called the counting numbers.The concept of “one sheep” came easily, then “two sheep,” “three sheep,” but people very quickly became convinced that this was too much work, and gave up counting at some point that they invariably called “many sheep.”These savvy thinkers immortalized the concept of zero (no sheep), and although they didn’t get around to naming all of the natural numbers, they figured out various systems whereby they could name them if they really wanted to using digits such as 1, 2, etc. This led to a burgeoning use of fractional numbers consisting of one integer divided by another, such as 2/3 or 111/27. Mathematicians called these rational numbers, and they fit in the number line in the obvious places between the integers. At some point, people became lazy and invented decimal notation, writing “3.1415” instead of the longer and more tedious 31415/10000
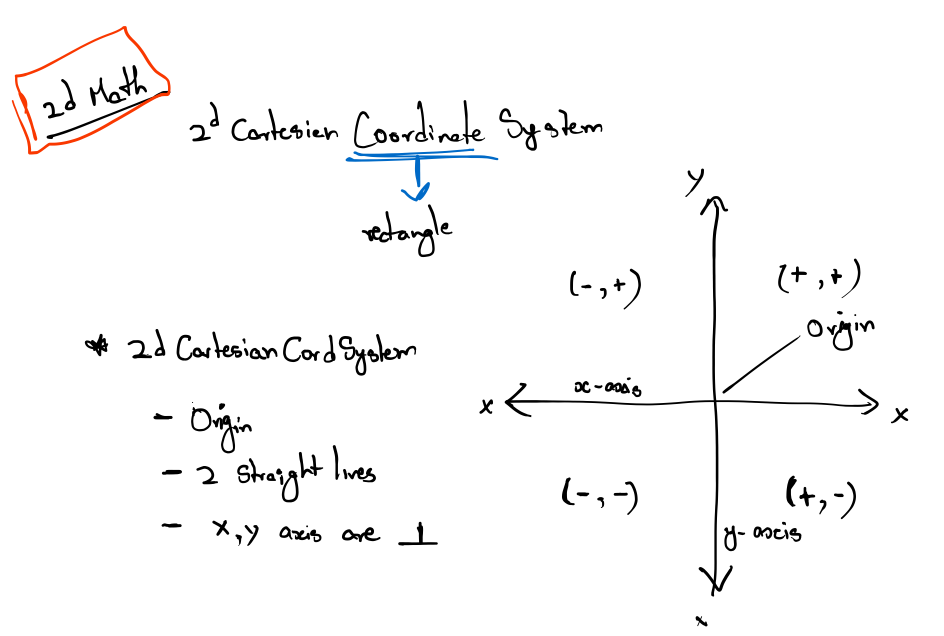
2D Cartesian Space
You probably have used 2D Cartesian coordinate systems even if you have never heard the term “Cartesian” before. “Cartesian” is mostly just a fancy word for “rectangular.”
3D Cartesian Space
The previous sections have explained how the Cartesian coordinate system works in 2D. Now it’s time to leave the flat 2D world and think about 3D space. It might seem at first that 3D space is only “50% more complicated” than 2D. After all, it’s just one more dimension, and we already had two. Unfortunately, this is not the case. For a variety of reasons, 3D space is more than incrementally more difficult than 2D space for humans to visualize and describe.
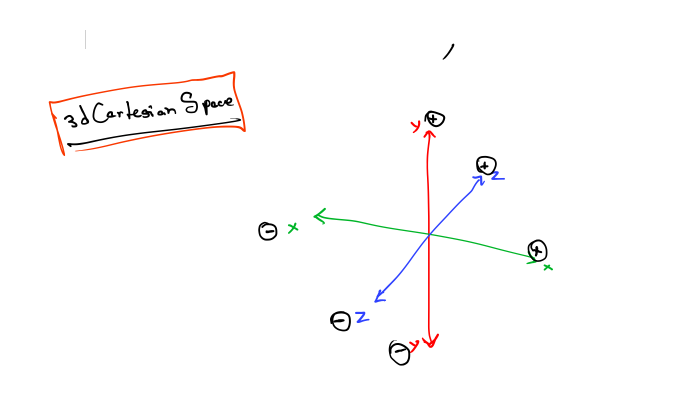
In 3D, we require three axes to establish a coordinate system. The first two axes are called the x-axis and y-axis, just as in 2D. (However, it is not accurate to say that these are the same as the 2D axes; more on this later.) We call the third axis (predictably) the z-axis. Usually, we set things up so that all axes are mutually perpendicular, that is, each one is perpendicular to the others.
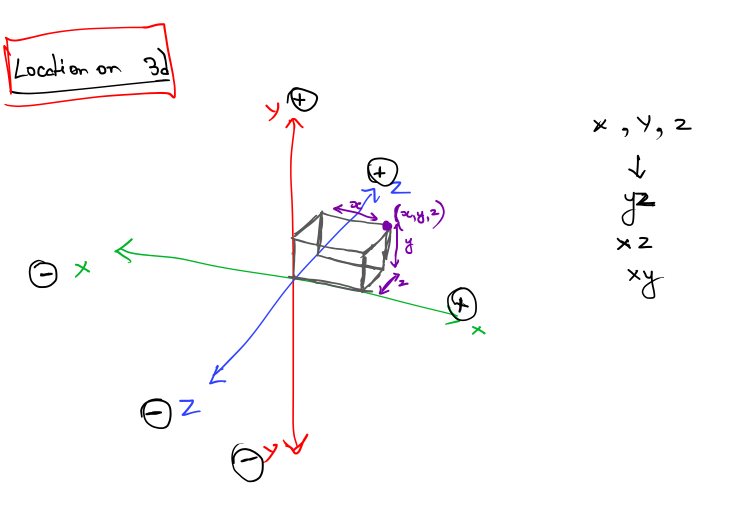
Location on 3D
In 3D, points are specified using three numbers, x, y, and z, which give the signed distance to the yz, xz, and xy planes, respectively. This distance is measured along a line parallel to the axis. For example, the x-value is the signed distance to the yz plane, measured along a line parallel to the x-axis.
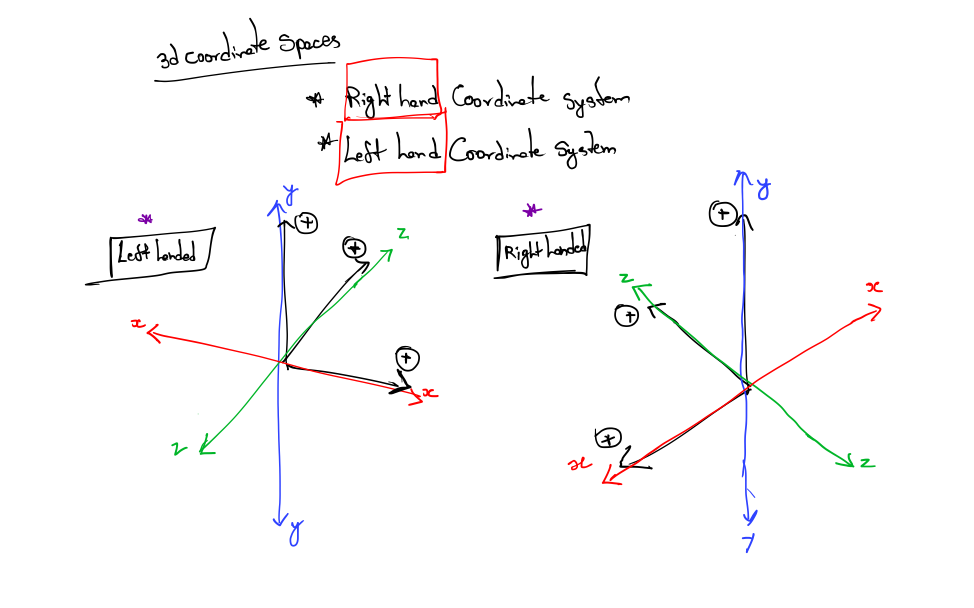
Left-handed versus Right-handed Coordinate Spaces
With your Left hand and Right hand your index finger should be pointing up. Now extend your third finger3 so it points directly forward. You have just formed a left-handed coordinate system. Your thumb, index finger, and third finger point in the +x, +y, and +z directions, respectively.
Left-handed and right-handed coordinate systems also differ in the definition of “positive rotation.” Let’s say we a have line in space and we need to rotate about this line by a specified angle. We call this line an axis of rotation, but don’t think that the word axis implies that we’re talking only about one of the cardinal axes (the x-, y-, or z-axis).
If you tell me to “rotate 30 degree about the axis,” how do I know which way to rotate? We need to agree between us that one direction of rotation is the positive direction, and the other di- rection is the negative direction.
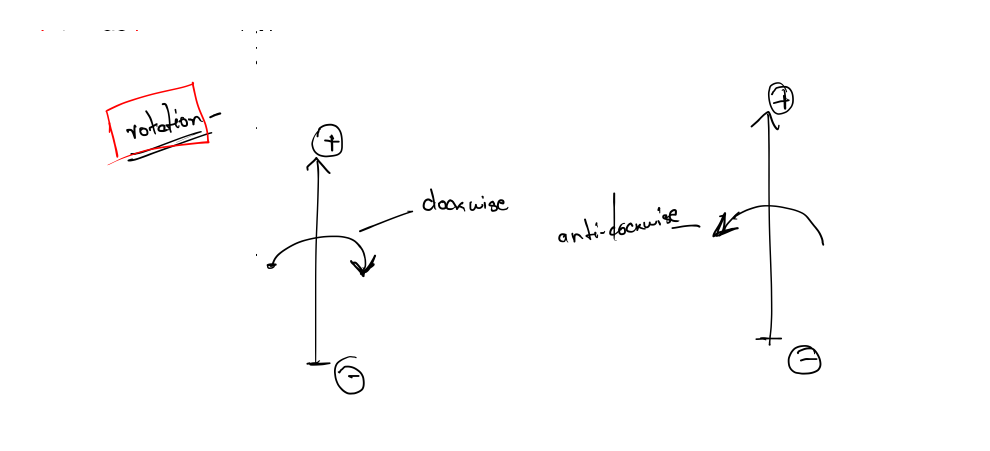
As you can see, in a left-handed coordinate system, positive rotation rotates clockwise when viewed from the positive end of the axis, and in a right-handed coordinate system, positive rotation is counterclockwise.
Odds and Ends
A few bits of mathematical knowledge, for a quick refresher.
Summation notation is a shorthand way to write the sum of a list of things. It’s sort of like a mathematical for loop.
i will count from 1 to 6. To “execute” our loop, we iterate the index through all the values specified by the control conditions. For each iteration, we evaluate the expression on the right-hand side of the summation notation (substituting the appropriate value for the index variable), and add this to our sum.
A similar notation is used when we are taking the product of a series of values,
Angles, Degrees, and Radians
An angle measures an amount of rotation in the plane.One degree measures 1/360 for a complete revolution.
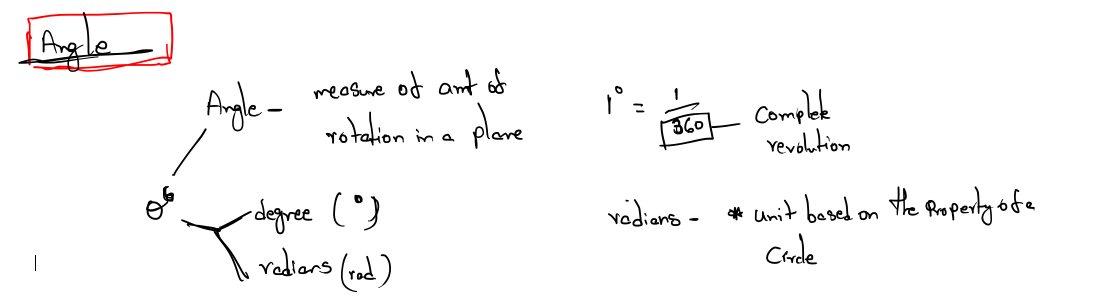
The circumference of a unit circle is 2π, with π approximately equal to 3.14159265359. Therefore, 2π radians represents a complete revolution.
Since 360 = 2π rad, 180 = π rad. To convert an angle from radians to degrees, we multiply by 180/π ≈ 57.29578, and to convert an angle from degrees to radians, we multiply by π/180 ≈ 0.01745329.
Thus,
1 rad = (180/π)o ≈ 57.29578o,
1o = (π/180) rad ≈ 0.01745329 rad.
Trignometry
There are many ways to define the elementary trig functions.In two dimensions, if we begin with a unit ray pointing towards +x, and then rotate this ray counterclockwise by an angle θ, we have drawn the angle in the standard position. (If the angle is negative, rotate the ray in the other direction.)
The (x,y) coordinates of the endpoint of a ray thus rotated have spe- cial properties and are so significant mathematically that they have been assigned special functions, known as the cosine and sine of the angle.
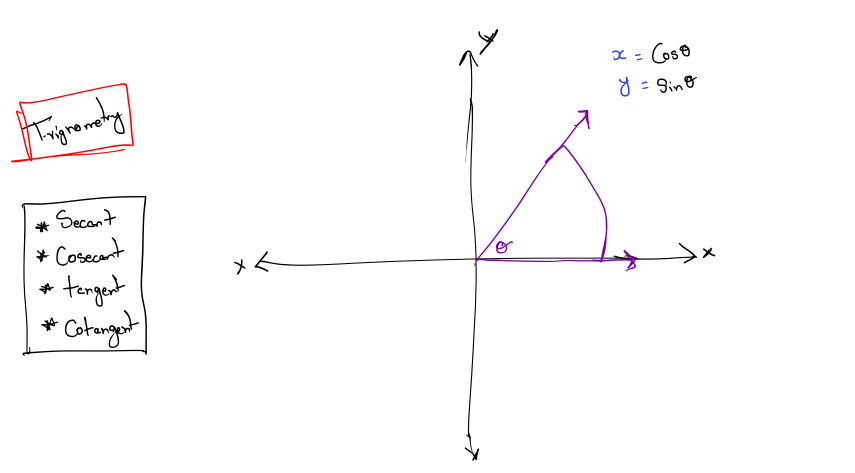
Primary Trig Functions are-
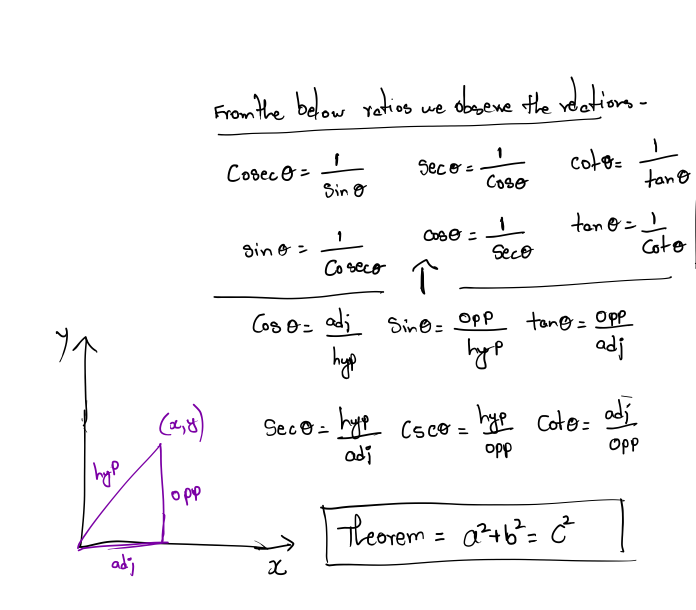
A number of identities can be derived based on the symmetry of the unit circle:
0-90 degrees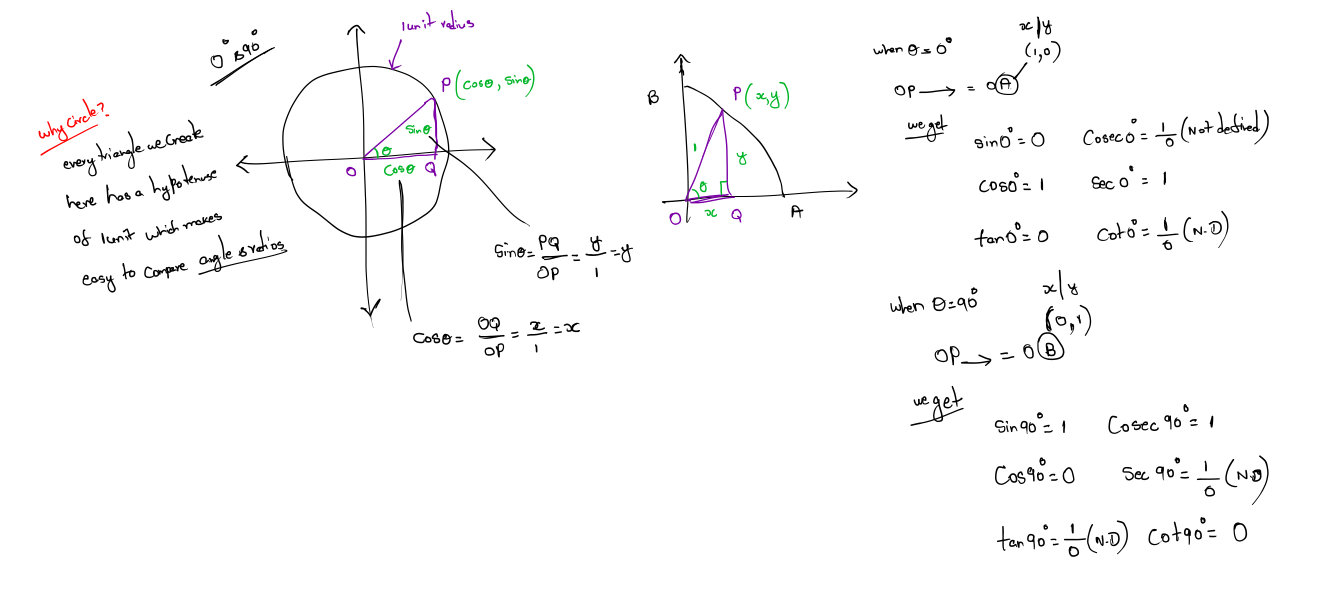
30-60 degrees
45 degrees
